Physical Computing
Final Project video
Still writing some documentation...
Still writing some documentation...
I connected the pins to Arduino as such:

Copied!#define BUTTON 2 #define LED_0 7 #define LED_1 8 int buttonValue; int ledState = 0; int lock = 0; void setup() { pinMode(BUTTON, INPUT); pinMode(LED_0, OUTPUT); pinMode(LED_1, OUTPUT); } void loop() { buttonValue = digitalRead(BUTTON); if (lock == 0 && buttonValue == HIGH) { lock = 1; // hold the lock delay(5); // sleep for 5ms /* do a second check after 5ms. this shouldn't be necessary with the lock in place, but the button seems too sensitive otherwise */ if (buttonValue == HIGH) { ledState++; if (ledState > 2) { ledState = 0; } } } // release the lock if we're not pressing the button if (buttonValue == LOW) { lock = 0; } // switch-case (maybe) a bit more readable than if-else-if switch(ledState) { case 1: digitalWrite(LED_0, HIGH); break; case 2: digitalWrite(LED_1, HIGH); break; default: digitalWrite(LED_0, LOW); digitalWrite(LED_1, LOW); break; } delay(5); }
I check that the button is being held two times with 5ms in-between (so that the button has hopefully been held for at least 5ms) at line 26.
This isn't strictly necessary, but as you can maybe see from the video below – the button I have feels a bit too sensitive. I felt it improved the control a little bit.
// END
I like the simplicity of Bruce and Box from the 2020 GDC list – showing that you don't need an interaction or the material/tools to be super complex to be fun for the players – especially when the setting is fun/absurd.
Bruce and Box is a simple game where you suddenly find yourself naked and try to get home by sneaking inside a cardboard box before you're caught. It works by using a distance sensor to calculate the distance between the floor and the cardboard box. The further you are away from the ground, the faster you go. The game probably pays homage to sneaking with the cardboard box in the classic game Metal Gear Solid.
My concept involves an upside bicycle with an IMU sensor attached to the wheelrim. The IMU sensor is used to sense whether the wheel is turning clockwise or counter-clockwise and at what speed, corresponding to left and right movement in a simple platforming game such as Super Mario Bros. The game would be a modified version of Super Mario Bros., where the faster you make the wheel turn, the faster your movement to that direction is.
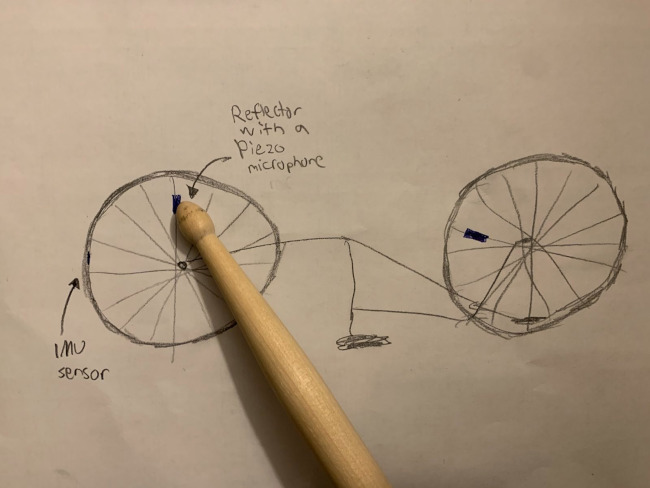
There is one of those classic yellow reflectors attached to one of the spokes in the wheel. A piezo microphone is set up to pick up hits on that particular spoke. In the hypothetical game you would use a drumstick to hit the spoke with the reflector in order to jump. There would be no speed limit in this game – the faster you rotate, the faster you can go – however jumping becomes really hard if you're rotating the wheel too fast in any direction, making controlling the game a careful, balancing act.
The fun part in this hypothetical game is that you could have two players side by side – each controlling one wheel of the bicycle, competing to play levels of the game as fast as possible.
Euclidean rhythms are rhythms that are spaced as evenly as possible. First described in a paper by Toussaint (2005), they are found in traditional music all over the world. For example the Cuban tresillo, humorously portrayed here, can be described by the Euclidean algorithm as:
E(3, 8) = 1 0 0 1 0 0 1 0
where k=3 is the number of hits and n=8 is the length of the rhythm.
I've previously played around some with Euclidean rhythms and found that they're quite nice to use if you use controllers to map values of k and n. That led to the idea of using servomotors to act as a rhythm machine.
The servomotor I have takes values from 0-180 corresponding to degrees in angles. My goal is to map each Euclidean rhythm to an angle. Instead of sending only 1s and 0s though, I can randomize the value of each hit to be a value between 1–180. Thus a hit with a value of 180 would be louder than a hit of 10, as the servomotor has to turn more and faster to reach the desired angle.
The tresillo rhythm with randomized accentuation could for example become:
10 0 0 20 0 0 10 0
which would indicate that the middle hit in the rhythm would be roughly twice as loud as the other hits.
How to do this kind of randomisation? Easiest would be of course to put a random value between 1–180 to each hit – but total randomness like this is rarely interesting. We want to have some control over the randomness, and to be potentially able to replicate a pattern that we like with a seed number we use.
Therefore, let's first constrain the problem by picking a few values that could be suitable for use with the servomotor. Through some experimentation, I found that 40 is enough to be the loudest, maximum value. I would argue that in traditional notated music, at least four values are needed for a wide enough dynamic range, piano, mezzopiano, mezzoforte and forte. If 40 is our forte, 20, 10 and 5 could represent the rest of the dynamics. What is needed then, is a function to generate all of the possibilities for our four dynamics. I've done a similar algorithm before to generate juggling patterns - this one was an easier version of that.
We start by noting that since our rhythms will be looping, there is a lot of redundancy in the patterns. For example, 20 10 5 40 is the exact same rhythm as 40 20 10 5, just rotated left once.
In fact we could take this even further and treat 40 20 10 5 as the same pattern as 40 5 10 20 even though this is actually not true. By adding a simple shuffle it's possible to generate the latter pattern from the same numbers as the previous one as well. What we're looking for is an algorithm to generate permutations that are sorted. As far as I know, there is no standard naming convention for these kind of permutations, but it is the same problem as described here.
It's quite easy to produce a few examples to gain some understanding how to generate a list of these numbers. We can try for example patterns with k=3 hits with our j=4 different amplitude choices (5, 10, 20, 40). Working by hand we get the following numbers:
40 40 40
40 40 20
40 40 10
40 40 5
40 20 20
40 20 10
40 20 5
40 10 10
40 10 5
40 5 5
20 20 20
20 20 10
20 20 5
20 10 10
20 10 5
20 5 5
10 10 10
10 10 5
10 5 5
5 5 5Using Python we can be sure that we generated all of the possible patterns by hand - as we have 20 of them, as expected.

Looking at the numbers we can split the algorithm into five different parts:

Voilà – we have an algorithm to generate all possible, sorted patterns. We can later on add additional constraints to choose our patterns. For example we could only choose patterns that don't contain any repeated numbers, patterns that sum to less than a certain amount, etc.
As a final step, remember to shuffle the sorted patterns to obtain all possible patterns.
Let's quickly recap what we are working with currently.
Now, there's an easy way to add volume control to our setup. We can divide the generated pattern and round to the nearest integer. For example, divide "40 0 0 20 0 0 5 0" by 5 and you get:
8 0 0 4 0 0 1 0
Again – these numbers correspond to servomotor angles in degrees. Asking the servomotor to turn a smaller angle makes a smaller mechanical sound since the servomotor has to turn less, and less quickly.
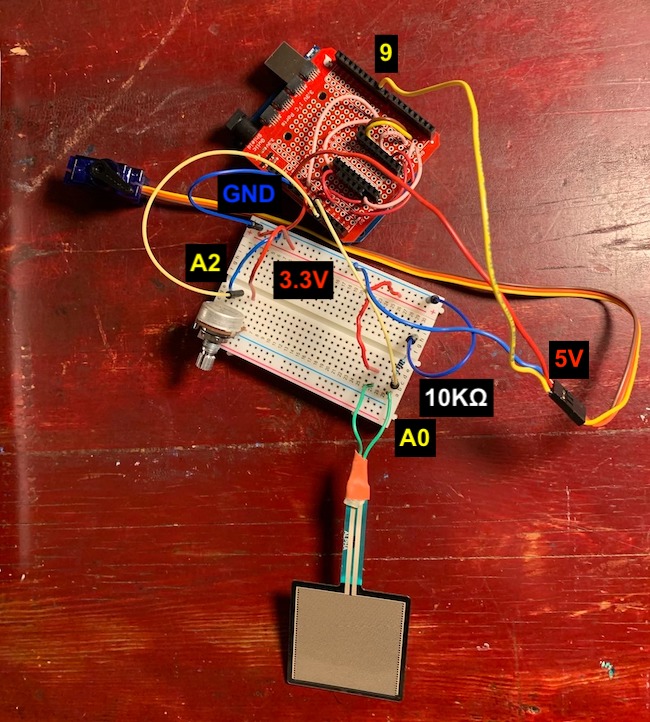
I added two sensors – a force-sensing resistor and a 10KΩ potentiometer. The force-sensing resistor acts like volume control as discussed in the previous section, and the potentiometer controls the Euclidean algorithm's parameters, namely the length of the rhythm, or n. The k parameter of the Euclidean algorithm is randomized.
The rhythms are generated inside SuperCollider code. SuperCollider is used to start the communication, and it reads four bytes at a time, of which the first two correspond to the touch sensor and the last two to the potentiometer values. Arduino then reads servo angles that are produced by the pattern it receives from Supercollider.
The end result. Unmute to hear the sound...
Here's the Arduino code:
Copied!#include <Servo.h> #include <Ewma.h> #define TOUCH_SENSOR_PIN A0 #define POT_PIN A2 #define SERVO_PIN 9 int touchValue; int filteredTouch; int potValue; int filteredPot; int pos; Ewma ewmaTouch(0.01); Ewma ewmaPot(0.01); Servo servo; void turnServo(long pos) { servo.write(pos); } void setup() { servo.attach(SERVO_PIN); Serial.begin(115200); } void loop() { // read two sensors touchValue = analogRead(TOUCH_SENSOR_PIN); potValue = analogRead(POT_PIN); // use filtering to smoothen the data filteredTouch = ewmaTouch.filter(touchValue); filteredPot = ewmaPot.filter(potValue); // send sensor data to Supercollider if (filteredTouch > 0) { Serial.write(highByte(filteredTouch)); // send higher byte Serial.write(lowByte(filteredTouch)); // then lower byte // Serial.println(); Serial.write(highByte(filteredPot)); // send higher byte Serial.write(lowByte(filteredPot)); // then lower byte } // read servo angles from Supercollider if (Serial.available() > 0) { pos = Serial.read(); turnServo(pos); // turn servo } delay(1); }
and finally the SuperCollider code.
Copied!// servo rhythms! ( /************************************* CONFIGURATION *************************************/ var serialport = "/dev/cu.usbmodem14101"; var baudrate = 115200; // "constants" ~primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101]; ~randSeed = 0; /***************************************** GUI *******************************************/ Window.closeAll; w = Window( name: "Servo", bounds: Rect(0, 0, 800, 300), ).front; w.alwaysOnTop = true; v = VLayoutView(w, Rect(10, 25, 800, 70)); h = HLayoutView(w, Rect(50, 70, 750, 230)); ~slider_touch = EZSlider( parent: h, bounds: 50@200, label: "Touch", controlSpec: ControlSpec(30, 600), layout: \vert, ); ~slider_pot = EZSlider( parent: h, bounds: 50@200, label: "Pot", controlSpec: ControlSpec(0, 10), layout: \vert, ); ~random_num = Button( parent: h, bounds: 100@100, ); ~random_num.string = "Randomize"; ~random_num.states = [["Randomize", Color.black, Color.rand]]; ~random_num.action = { ~randSeed = rrand(0, 9999); thisThread.randSeed = ~randSeed; ~randomizeRhythm.(~randSeed, ~primes[~slider_pot.value]); ~random_num.states = [["Randomize", Color.black, Color.rand]]; }; ~random_text = StaticText(v); ~rhythm_text = StaticText(v); /************************************* FUNCTIONS *****************************************/ // generate servo rhythms with length n from maxim to minim // dividing the rhythm by 2 each time // this will generate exactly binom(n+k-1, n) rhythms // where k is the number of rhythm choices // // e.g. n=2, maxim=20, minim=5 would generate // // [20, 20] // [20, 10] // [20, 5] // [10, 10] // [10, 5] // [5, 5] // // here we have binom(2+3-1, 2) = 6 rhythms generated since we have k=3 choices [5, 10, 20] // see: https://math.stackexchange.com/q/2608264 ~generateServoRhythms = { |n, maxim=40, minim=5| var rhythms, arr, i; rhythms = List(); arr = maxim!n; block { |break| while ({ true }, { rhythms.add(arr.copy); i = n - 1; while ({ arr[i] > minim }, { arr[i] = arr[i].div(2); rhythms.add(arr.copy); }); while ({ (i >= 0) and: (arr[i] == minim) }, { i = i - 1; }); if (i < 0, { break.(rhythms); }); arr[i..] = arr[i].div(2); }); }; }; // this function creates random rhythms with rhythmical variation // // first of all we use the Bjorklund algorithm to generate euclidean rhythms // euclidean rhythms are rhythms that are distributed as evenly as possible // see: http://cgm.cs.mcgill.ca/~godfried/publications/banff.pdf // // Bjorklund algorithm usage: Bjorklund(k, n), where // k = the number of hits and n = the length of the rhythm // // for example Bjorklund(2, 5) creates always two hits spaced like so: // [1, 0, 1, 0, 0] // here 1 denotes a hit // // we modify Bjorklund's algorithm by giving some random rhythmical variations // that we then send to a servomotor // // a servomotor accepts values from 0-180 (angle in degrees) // // we could therefore for example modify the previous two hits to be: // [ 10, 0, 5, 0, 0 ] // so that the first hit is stronger than the previous one (more servomotor movement = more sound) ~generateServoAmps = { |k=4, n=9, maxRhythmSum| var i = -1; var servo; if (maxRhythmSum.isNil, { maxRhythmSum = (k+1) * 20; }); servo = ~generateServoRhythms.(k).select({ |x| sum(x) <= maxRhythmSum }).choose.scramble; Bjorklund(k, n).collect({ |x| if (x == 1, { i = i + 1; servo[i]; }, { 0 }); }) }; ~randomizeRhythm = { |seed, timeSignature| thisThread.randSeed = seed * ~randSeed; ~rhythm = ~generateServoAmps.( rrand(1, (0.75 * timeSignature).round.asInteger), timeSignature, ); Pdefn(\angle, Pseq(~rhythm, inf)); }; /********************************* SERIAL COMMUNICATION *********************************/ if (~serial.notNil, { ~serial.close }); ~serial = SerialPort( port: serialport, baudrate: baudrate, ); CmdPeriod.add({ fork { ~serial.put(1); 0.1.wait; ~serial.close; } }); // listen to serial data fork { var bytes; var touch, pot; var touchScaled, potScaled; var timeSignature; var prevPot = -1; loop { bytes = [-1, -1, -1, -1]; 4.do({ |i| bytes[i] = ~serial.read; }); touch = bytes[0] << 8 | bytes[1]; pot = bytes[2] << 8 | bytes[3]; touchScaled = touch.lincurve(30, 600, 8, 0.125, -6); potScaled = (pot.round(20)).linlin(0, 700, 0, 10).round.asInteger; timeSignature = ~primes[potScaled]; if (prevPot != potScaled, { ~randomizeRhythm.(potScaled, timeSignature); prevPot = potScaled; }); // update GUI AppClock.sched(0.0, { ~slider_touch.value = touch; ~slider_pot.value = potScaled; ~rhythm_text.string = ~rhythm.div(touchScaled).min(180); ~random_text.string = "Random seed: " + ~randSeed; }); Pdefn(\div, touchScaled); } }; // create a handle to be able to control tempo later t = TempoClock.default; t.tempo = 60/60; // our pattern p = Pbind( \dur, 0.125, \div, Pdefn(\div), \angle, Pdefn(\angle), \play, { topEnvironment.at(\serial).put(~angle.div(~div).min(180)); }, ).play(t); )
// END


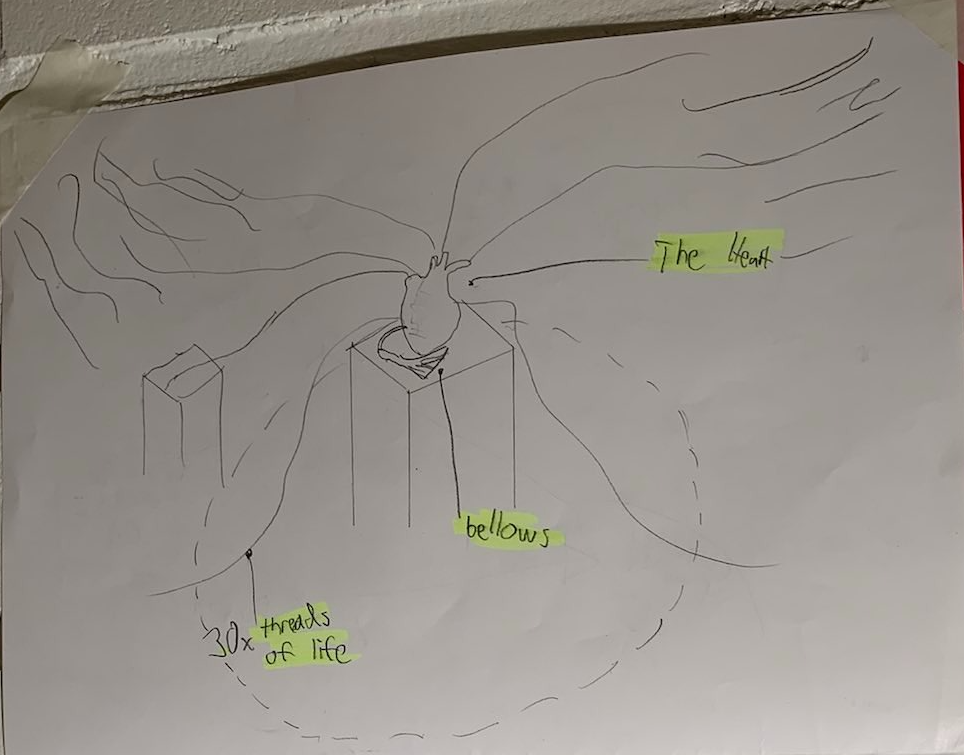
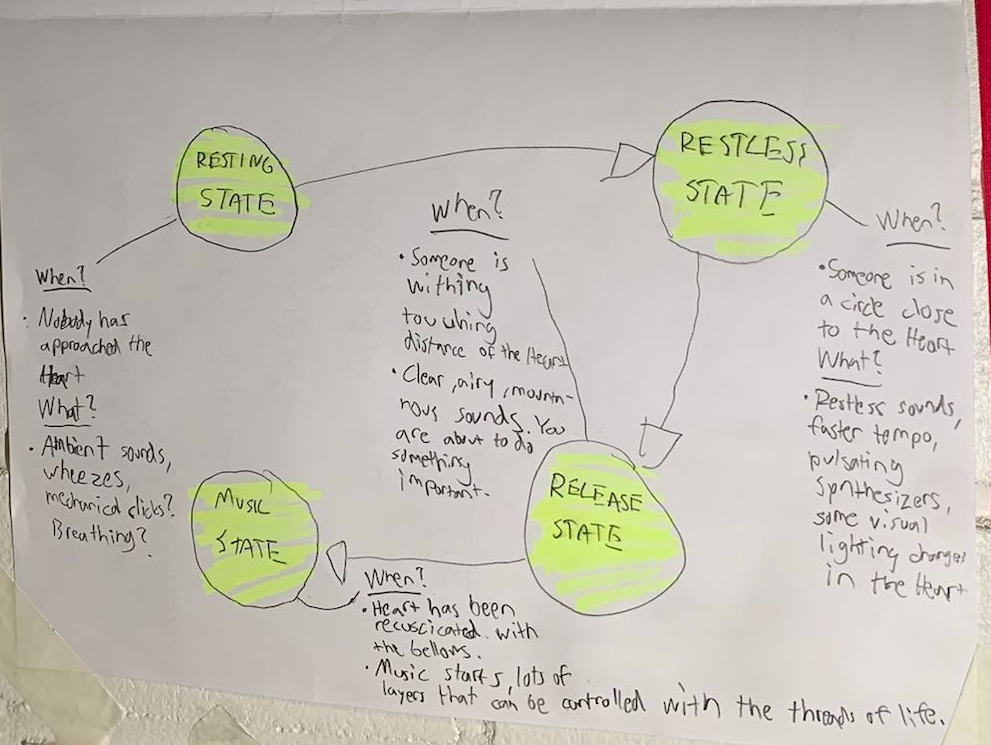
My final project is to explore the interactions and fabrication necessary for my master's thesis idea. For my thesis I plan to make a multichannel, interactive audio installation with a heart in the middle of a room.
When a person enters the room there is an ambient soundscape of wheezing, clicking, mechanized sounds, breathing. People can explore the auditory scene of the room without interacting if they so wish.
When the person approaches The Heart, raw, restless synthesized pulsating sounds appear, which become higher and higher in volume, trying to guide the person towards The Heart.
When the person finally is within touching distance from The Heart, there should be a change in the audio scenery like you were suddenly on top of a windy mountain, a release of tension, and a light will turn on inside The Heart, signifying you to interact with it.
Finally, if a person interacts with The Heart to resuscitate it, music starts playing. There are strings similar to veins called threads of life coming out of The Heart and filling the room. Some of them are on a highlighted spot, such as on top of a pedestal, accompanied by a nearby speaker. While the music is playing, if a person touches a thread of life, an additional layer to the music will fade in and start playing from the closest speaker.
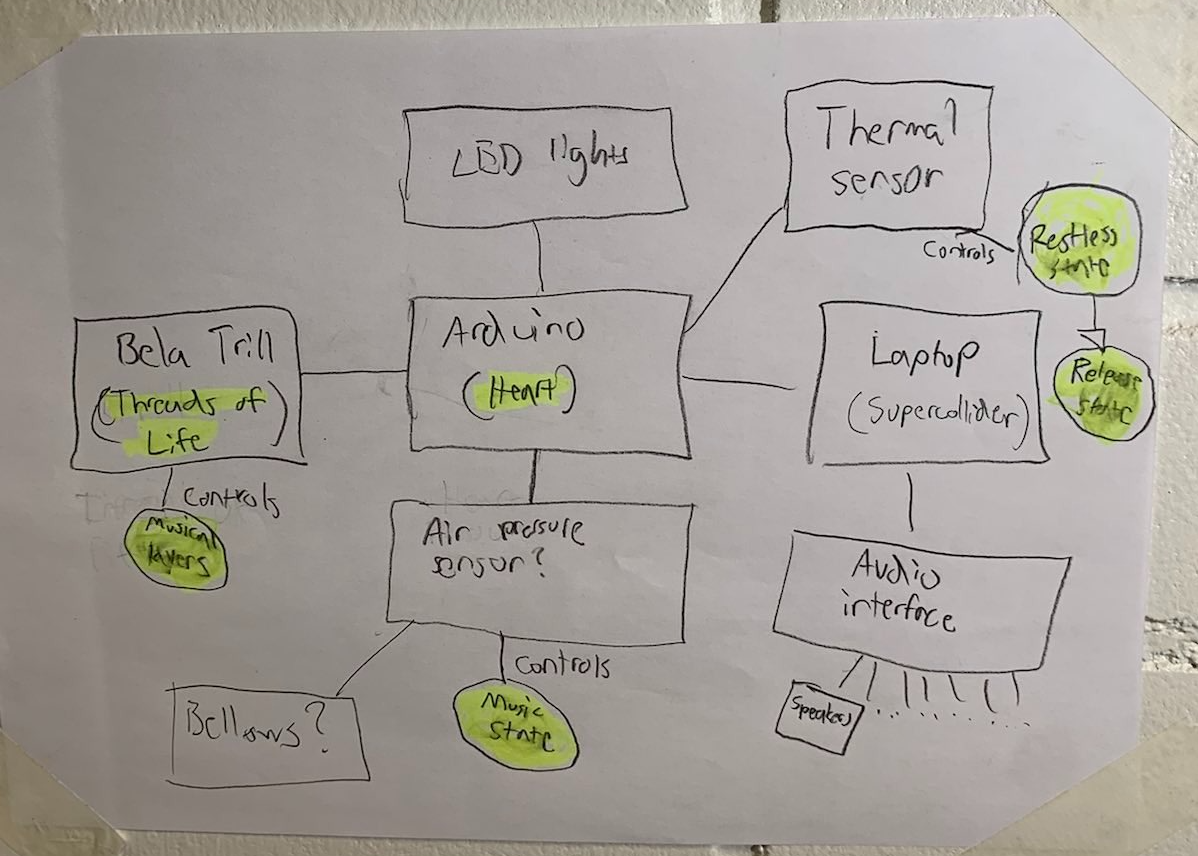
I'm starting the project from scratch as I do the final project for this course. The goal is to at least prototype a few interactions, figure out how do they work, as well as explore the fabrications necessary to make the installation work.
I don't have a lot of previous experience with electronics or fabrication. I did one major project previously where two infrared sensors were used to detect a person either entering or exiting an elevator - and if they were exiting the elevator - some sounds were played through eight surface transducers. This was exhibited over the last summer for three months.
I'll focus on The Heart and threads of life interactions and also explore the visual look for the installation. I also want to at least try out the distance sensing.
// END
Jasmine Xie, a recent Aalto University graduate has made an amazingly well documented tutorial on how to make and cast a silicone mold.
// END
to be written...
// END
Total: $141
My end goal with the distance sensing is to be able to sense how close an audience member is to The Heart, which is situated in the middle of the room. If the music is not already playing, there is an ambient soundscape that should interactively change in order to guide the audience towards interacting with The Heart.
What I require from the distance sensing is two things:
Distance sensing could be done in many ways, for example by using optical cameras and computer vision. A thermal sensor is a computationally cheap option that might also work well for this type of application.

The MLX90640 is a thermal sensor that works by passively picking up mid-to long wavelength infrared radiation. It has a 32x24 pixel array with up to 64Hz refresh rate – although for some reason I managed to only get up to 16Hz working. The accuracy is roughly ±1.5°C under ideal conditions.
The actual image it sees is not rectangular, as the image is distorted by the lens. The 55° FOV sensor seems to have a pincushion distortion, and I'm guessing the 110° wide lense will have barrel distortion.
It also seems like the sensor is skewed so that the image is rotated when the board is mounted parallel to a room. I'll still have to test how big the skew actually is in order to rotate it properly.
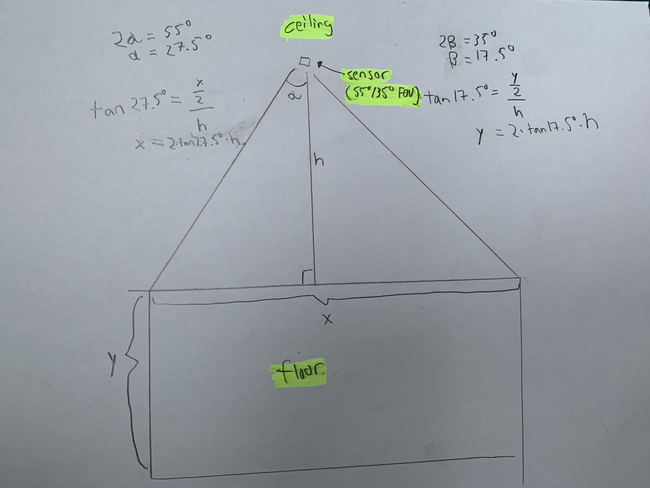
The thermal sensor can be mounted on top of an object in the ceiling in order to sense distance from the center of an object. Using basic trigonometry one can then calculate the area the sensor will see. I've made a calculator below to do these calculations automatically.
The I²C cable can't transfer data over longer distances as it starts to pick up too much noise. It's possible to extend the cable using an ethernet (CAT5) cable for example with the Sparkfun QwiicBuses. Since the sensor in my case needs to be installed into the ceiling, I had to use them.

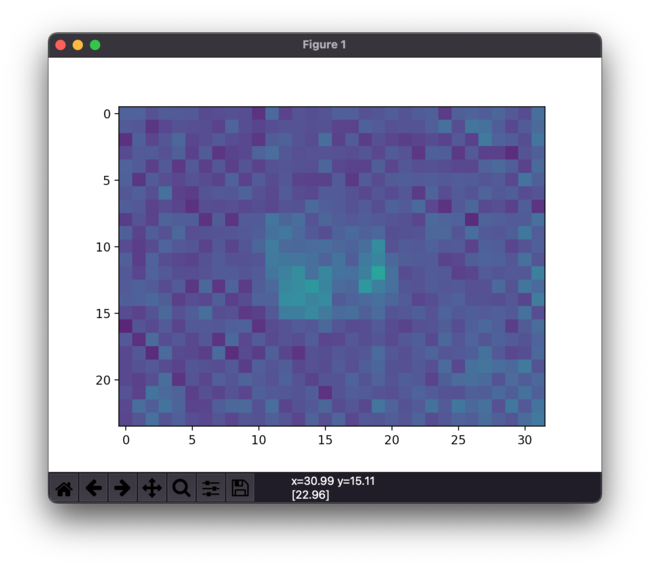
The problem with using thermal sensors in Finland is that during winter time people might be wearing winter clothes. The difference in the amount of heat emitted is significant and has to be taken into account when using the sensor.
Working with a thermal sensor is fun as you can use a water cooker when calibrating the sensor area :)

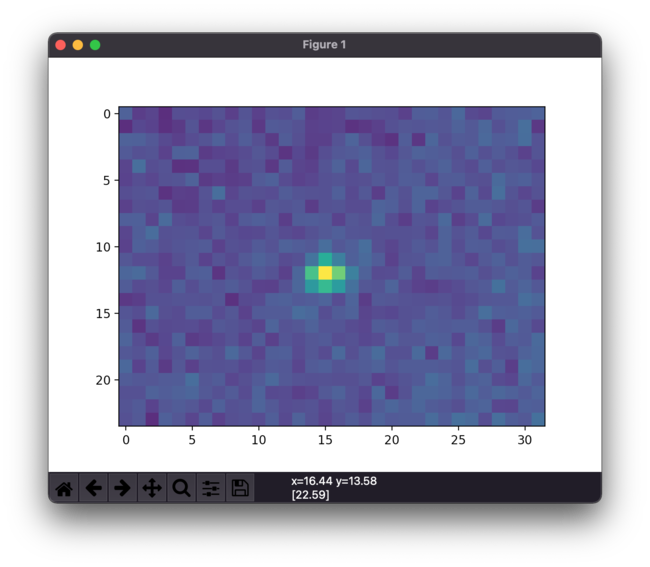
To read data from MLX90640 you need a more powerful microcontroller than a traditional Arduino Uno. I tried the sensor with a Teensy 3.5 and got it working with a maximum of 16Hz refresh rate. I did some timing tests and it seems like for whatever reason I only get data roughly every 1/8th of a second with the 16Hz refresh rate.
To use the Arduino IDE with Teensys, you need to go to the Arduino IDE preferences and add a URL for additional board managers:
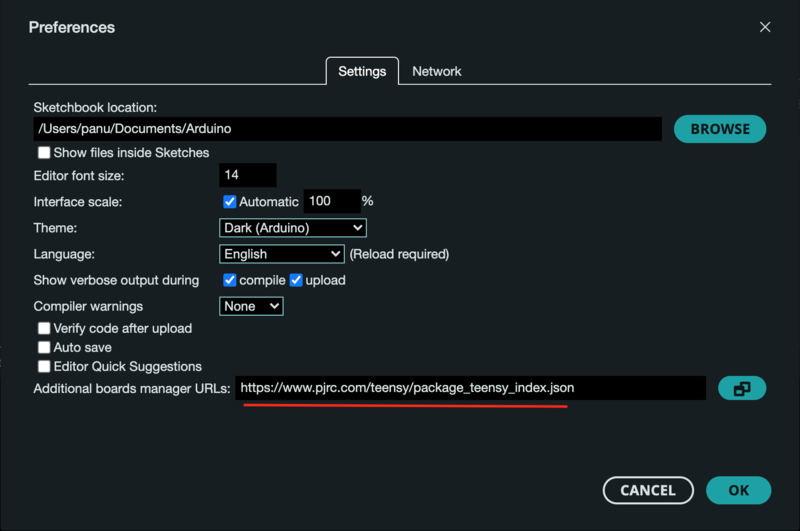
and then use the Boards Manager to install Teensy.
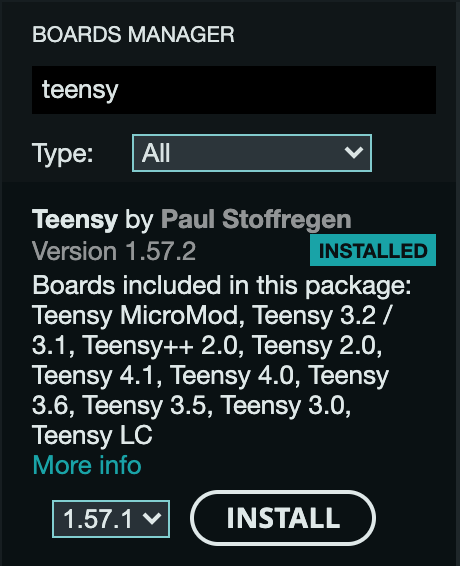
Adafruit has a library for MLX90640 that we can use to read data. Here's code to send a frame (32x24 = 768 pixels) of sensor data over serial:
Copied!#include <Adafruit_MLX90640.h> Adafruit_MLX90640 mlx; float frame[32*24]; // buffer for a full frame of temperatures byte byte_array[32*24*sizeof(float)]; // bytes to be sent over serial communication // send the IR sensor frame through serial void sendFrame() { memcpy(byte_array, frame, sizeof(byte_array)); Serial.write(byte_array, sizeof(byte_array)); } void setup() { while (!Serial) delay(10); Serial.begin(230400); delay(100); if (!mlx.begin(MLX90640_I2CADDR_DEFAULT, &Wire)) { Serial.println("MLX90640 not found!"); while (1) delay(10); } Wire.setClock(1000000); // 1 MHz clock speed is the maximum MLX90640 can support mlx.setMode(MLX90640_CHESS); // MLX90640 datasheet recommends using the chess pattern mlx.setResolution(MLX90640_ADC_19BIT); // internal resolution, more bits = less noise mlx.setRefreshRate(MLX90640_16_HZ); // update rate } void loop() { // if we get a frame, send it if (mlx.getFrame(frame) == 0) { sendFrame(); } }
python with its numpy module is probably the best option to use when processing two-dimensional matrix data. I've made a python script with various options to process the MLX90640 data (reminder to self: add the script below).
To detect a single person's location with the sensor setup as above, it's best to take an average over a few pixels that would roughly correspond to a person's size. This is easiest to achieve using convolution. This makes tracking people under much more smoother and less prone to noise in the data.
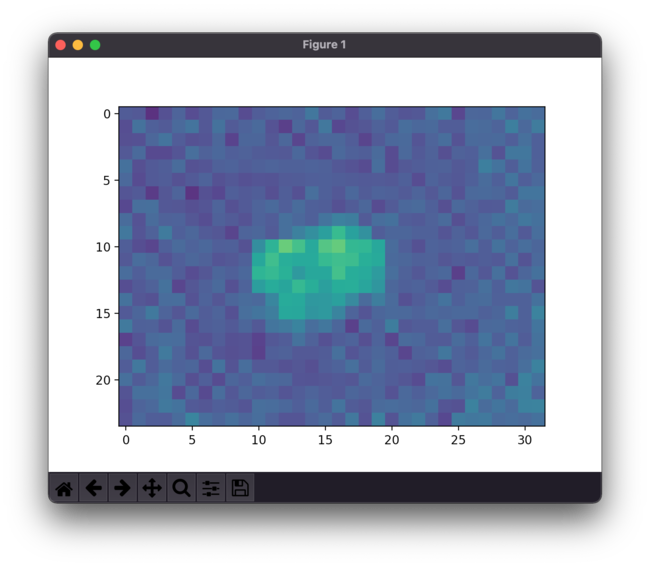
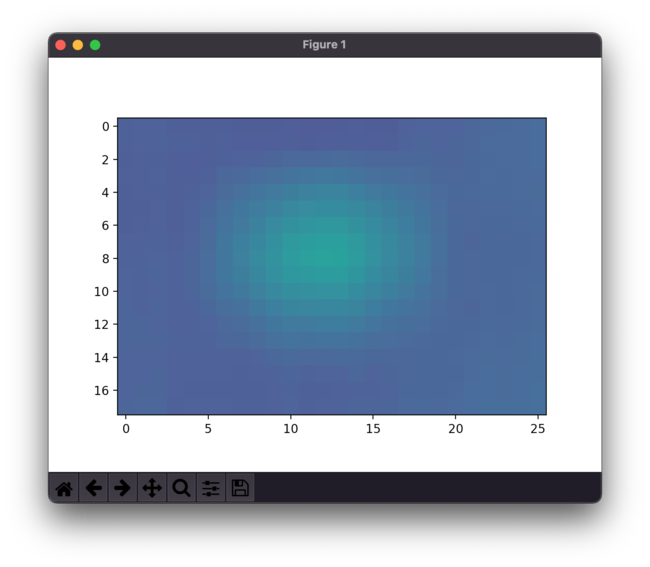
// END